线段树
简述何为线段树
简单来说,是通过原数组生成一个的一个二叉树,其中,树的每一个非叶子节点都是由其子节点通过一些算数运算生成的,比如求解区间和,就是每个节点对子节点求和生成的,每个节点存储的就是子节点的和,
(node.value = node.left.value + node.right.value)
或者区间最大值的树,就是取其中最大值生成的,每个节点就是子节点中的最大值
(node.value = max(node.left.value, node.right.value))
线段树从叶子依次向上生成的。那么来说,每个非叶子节点的值
就是代表所有子节点的的有效值(或者说是特征(最大最小))的节点,每个节点代表的区间就是对应着所有子节点区间的合并区间。
例如叶子节点为原数组的值,那么其父节点的值就是其与兄弟节点的和(或者取最大最小值),
其父节点的所代表的区间就是其节点的区间与兄弟节点的区间的合并区间。
(因为每个叶子节点代表的区间就是他自己本身,所以其节点的区间与兄弟节点的区间的合并区间就是它们本身)
其逻辑结构形如下图 (区间和的线段树):
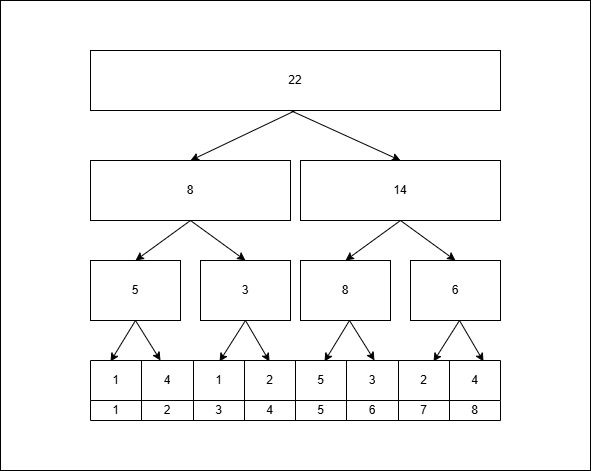
但是线段树以顺序表存储会处理更加方便,所以采用顺序结构存储,其存储结构形如下图,
| root | node 1 | node 2 | ... | 原数组元素 0 | 原数组元素 1 | ... | 原数组元素 n |
其中每一个节点都有四个属性:
- start : 节点所代表区间的开始地址
- end : 节点所代表区间的结束地址
- value : 节点所代表区间的总有效值
- lazy : 节点所代表区间的修改值
其中根节点为坐标为0,每一个地址为i的节点的左右孩子地址分别为i*2与i*2+1,父节点为i/2,
其中线段树的主要作用是数组区间频繁查询或修改
区间频繁查询:
查询涉及分治思想,分解,解决,合并。
若要查找的区间[l,r]与当前节点所包含的区间[start,end]完全相同
(即node.start=l 且node.end=r)
那么直接返回当前节点的值,因为当前节点就代表其包含区间的总有效值
若是从树顶至下查找区间[l,r]并不是与当前节点完全相同,那么无非三种情况,
- 要查找区间完全在当前节点完全在当前节点的左节点的区间
- 那么直接递归进入左子树继续查询
- 要查找区间完全在当前节点完全在当前节点的右节点的区间
- 那么直接递归进入右子树继续查询
- 要查找区间完全在一部分在左节点的区间,一部在右节点的区间
- 将要查找的区间
[l,r]分为两部分[l, m]与[m,r]其中m = (l+r)/2, - 再对左子树查询
[l,m],右子树查找[m,r]
- 将要查找的区间
以上情况会一直递归至要查找的区间[l,r]与当前节点所包含的区间[start,end]完全相同
那么就会递归返回其节点的值,其值即为最终的值。
区间频繁修改
区间频繁修改需要给每个节点添加一个新的属性lazy,
每个节点的lazy属性标志着其区间的修改标志,
例如,在一棵对于求区间和的线段树中,如果修改代表区间[l,r]区间的节点node的lazy为10
就代表在[l,r]这个区间中,每个值都添加10,但是不需要修改其所有子节点的值,只需要知道
当前节点的所有子节点个数n,再返回node.value + 10 * n即可。
设置区间的lazy的过程与查询区间相同,从线段树的根节点开始依次向下查找,
查找到符合区间的节点之后,设置其lazy属性即可。
单点查询与修改
单点查询
如果想要在树中查询某个元素(叶子节点)的值,那么从根节点开始向下查找
在递归的过程中,若在当前当前节点的区间已经被修改,即lazy不为0,
那么在递归查找子节点时,就需要把当前节点的lazy设置给子节点,并将当前节点的lazy置零
这个操作叫做下放pushdown
直至查找到要查询的节点元素时,通过lazy值来对当前节点的值修改
并把lazy置零,返回当前节点修改后的值
单点修改
单点修改在单点查询的基础上,找到要修改的节点元素,再对节点进行修改
之后,从当前节点向父节点递归修改父节点的值,直至根节点
因为对单个叶子节点进行修改,可能会改变包含本节点区间的节点的值
(也可能不会,比如在区间最大值的线段树中,修改后的节点值仍然比兄弟节点小),
所以需要对父节点进行递归修改。